[BAEKJOON ONLINE JUDGE 9663번] N-Queen

작성일 | In , , |

N-Queen

문제

  • N x N (칸) 크기의 체스판 위에 오직 N개의 Queen만을 서로를 공격할 수 없게 놓았을 때, 앞의 설명과 같이 Queen말을 놓는 모든 방법의 수를 구하여 출력한다.

입력 데이터

  • 체스판 한 변의 길이(혹은 Queen 말의 수) N
  • 입력 예
4

출력 데이터

  • N x N (칸) 크기의 체스판 위에 Queen말을 놓는 모든 방법의 수
  • 출력 예
2

조건

  • N은 1이사 15이하의 정수
  • Queen말은 자신과 같은 직선, 대각선에 위치한 말을 공격할 수 있음

해결 방법

  • 예를 들어 1 x 1 크기의 체스판에는 체스판의 크기도 1 x 1(1칸) 이지만, 놓을 Queen의 수도 1개 이므로 방법의 수는 (1, 1)에 놓는 1가지 이다.
  • 그러나 2 x 2 일 때와, 3 x 3 일 때는 Queen을 놓을 수 있는 방법이 존재하지 않는다.
    • 2 x 2 크기의 체스판에서 만약 (1, 1)에 Queen을 놓는다고 하면, (2, 1), (2 ,2) 두 칸 모두 Queen을 놓는 것이 불가능 하다. (1, 2)에 Queen을 놓았을 때도 마찬가지 이다.
    • 3 x 3 크기의 체스판에서도 2 x 2 크기의 체스판에서 처럼 계산 해보면 방법이 존재하지 않는다.
  • 4 x 4 크기의 체스판에서는 다시 방법이 존재한다.
    • 그 방법은 (1, 2), (2, 4), (3, 1), (4, 3)과 (1, 3), (2, 1), (3, 4), (4, 2)에 놓는 2가지 이다.
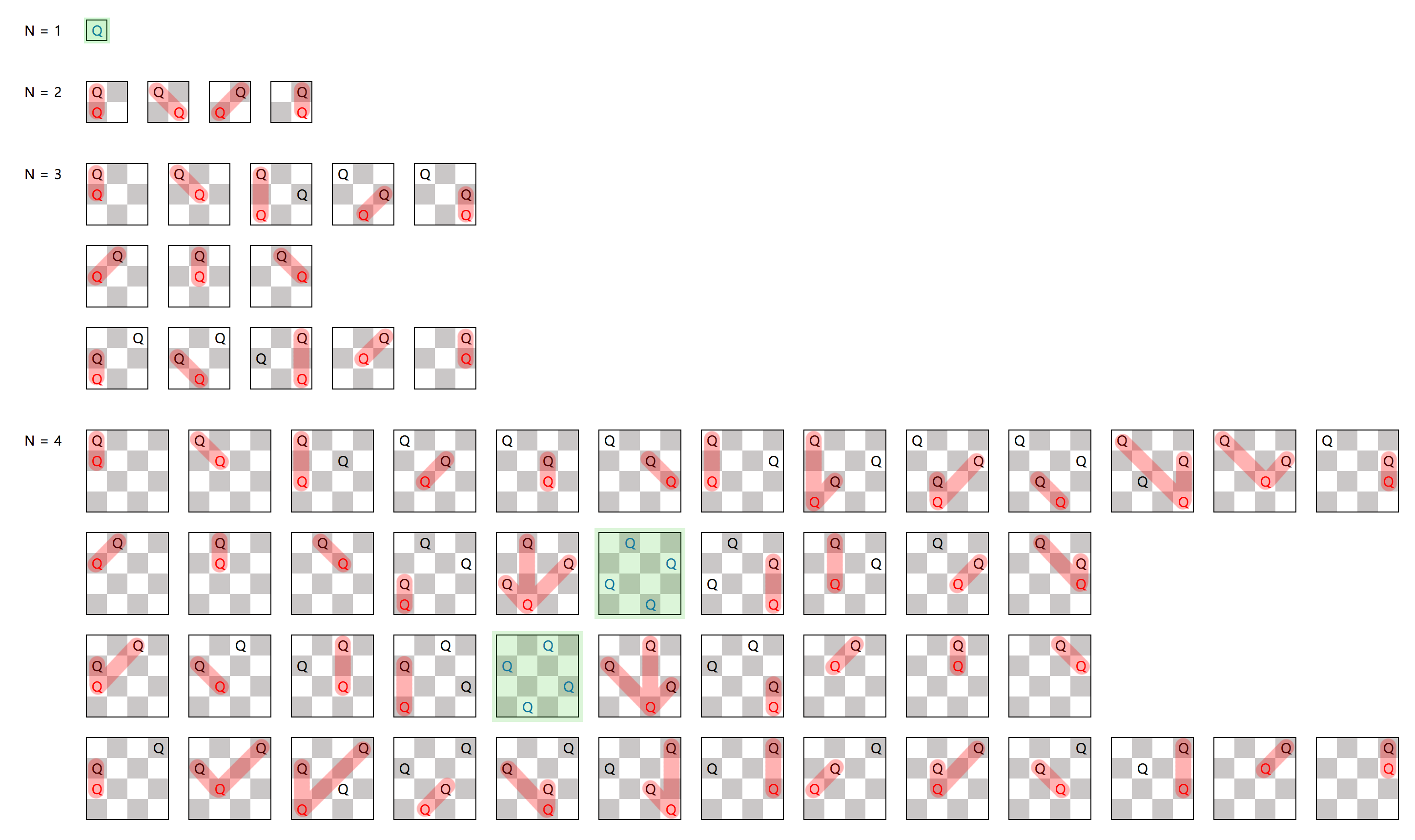
  • 이 설명을 아래의 그림에 나타내 보았다. No Image
    • 그림에서 Q는 Queen이며, 초록색으로 칠해진 체스판은 가능한 방법 이며, Q들 끼리 분홍색 선으로 그어진 것은 빨간색 Q를 놓았을 때 분홍색 선 상의 Q를 공격할 수 있어서 불가능한 방법을 나타낸다.
  • 위 그림과 같이 직접 하나하나 검사하여 확인해 보는 수 밖에 없다.

코드

  • C++ 이용

#include <iostream>
#include <cmath> // abs 함수 이용
using namespace std;

int N; // 체스판의 크기(N x N에서 N)
int count = 0; // 구하고자 하는 방법의 수
int *x; // 각 row에서 Queen의 위치를 저장할 동적 배열, ex) x[1]=2 라면, 1번째 row에서 Queen은 2번째 column에 있음

bool isPromising(int k, int col); // k번째 row에서 Queen이 col번째 column에 놓을 수 있는지 (k-1번째 row까지) 검사하는 함수
void nQueens(int k); // 문제 해결을 위한 함수

int main()
{
    cin >> N;

    x = new int [N + 1]; // x[1]부터 x[N]까지 사용을 하기 위해 배열 동적 할당

    for(int row = 0; row <= N; row++) // 배열 초기화
    {
        x[row] = 0;
    }

    nQueens(1); // 1번째 row부터 각 row와 column별로 검사하기 위해 nQueen(1)을 호출
    cout << count << endl;

    delete x; // 동적 할당 해제

    return 0;
}

bool isPromising(int k, int col)
{
    for(int row = 1; row < k; row++) // 1번째 row부터 k-1번째 row까지 검사
    {
        if((col == x[row]) || (abs(k - row) == abs(col - x[row]))) return false; // row번째 Queen과 놓으려는 Queen이 같은 직선이나 대각선 상에 있으면 해당 위치에는 Queen을 놓을 수 없음
    }
    return true; // 위의 조건에 해당되지 않으면, Queen을 해당 위치에 놓을 수 있는 것임
}

void nQueens(int k)
{
    for(int col = 1; col <= N; col++) // 1번째 column부터 N번째 column까지 일일히 검사
    {
        if(isPromising(k, col)) // k번째 row에서 col번째 column에 Queen을 놓을 수 있는 경우
        {
            x[k] = col; // k번째 row에서 Queen의 위치는 col번째 column임

            if(k < N) nQueens(k + 1); // 다음 row검사(nQueens함수 다시 호출)
            else count++; // 가능한 방법의 수 증가
        }
    }
}

  • Python 이용

# -*- coding: utf-8 -*-
# UTF-8 encoding when using korean

def isPromising(k, col): # k번째 row에서 Queen이 col번째 column에 놓을 수 있는지 (k-1번째 row까지) 검사하는 함수
    for row in range(1, k): # 1번째 row부터 k-1번째 row까지 검사
        if col == x[row] or abs(col - x[row]) == abs(k - row): # row번째 Queen과 놓으려는 Queen이 같은 직선이나 대각선 상에 있는 경우
            return False # 해당 위치에는 Queen을 놓을 수 없음
    return True # 위의 조건에 해당되지 않으면, Queen을 해당 위치에 놓을 수 있는 것임

def nQueens(k): # 문제 해결을 위한 함수
    global count # count변수는 전역 변수로 이용함
    for col in range(1, N + 1): # 1번째 column부터 N번째 column까지 일일히 검사
        if isPromising(k, col) == True: # k번째 row에서 col번째 column에 Queen을 놓을 수 있는 경우
            x[k] = col # k번째 row에서 Queen의 위치는 col번째 column임
            if k < N:
                nQueens(k + 1) # 다음 row검사(nQueens함수 다시 호출)
            else:
                count += 1 // 가능한 방법의 수 증가

count = 0 # 구하고자 하는 방법의 수
N = int(input()) # 체스판의 크기(N x N에서 N)
x = [0]*(n + 1) # x[1]부터 x[N]까지 사용을 하기 위해 배열 동적 할당
nQueens(1) # 1번째 row부터 각 row와 column별로 검사하기 위해 nQueen(1)을 호출
print(count)

문제 원본 링크

https://www.acmicpc.net/problem/9663

0%